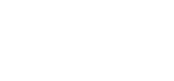I nie chodzi tu o skrzyżowanie blondynki z husky, ale o krzywą biegunową. Po tym niezbyt przemyślanym wstępie mogę przejść do sedna sprawy. Biegunowa jest podstawą do skutecznego latania przelotowego. Opisuje ona prostą zależność : ile mamy opadania przy danej prędkości.
Ze względu na specyfikę paralotni możemy skupić się nad pięcioma wartościami prędkości. Będą to: prędkość minimalna (V min) , prędkość najmniejszego opadania (V ek od ekonomiczna), prędkość największej doskonałości (V opt od optymalna) i dwie prędkości maksymalne na ½ speeda i na całym (V 1/2max i V max).
Jako materiału poglądowego będę posługiwał się danymi uzyskanymi w czasie prób skrzydła Shark. Dane uzyskano dla masy startowej 109 kg dla skrzydła o powierzchni 24,21 m2 w rzucie.
Dane z lotu zostały zaprezentowane na wykresie nr 1 i umożliwiły wykreślenie krzywej biegunowej (wykres nr 2) za pomocą programu komputerowego.
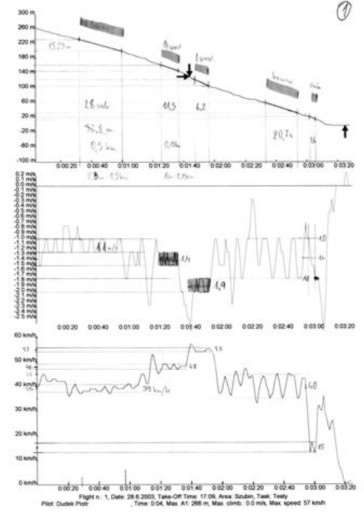

Ponieważ jednak program potrzebuje do wykreślenia biegunowej stabilnej prędkości opadania i postępowej, dlatego dokładność wykreślenia tej krzywej wymagała sprawdzenia. W tym celu wykorzystałem wspomniane wcześniej wykresy zapisu lotu, gdzie za pomocą ołówka uśredniłem wartości prędkości opadania i postępowej. Ponieważ na barogramce wykres lotu doskonale pokazywał kąt szybowania, to wystarczyło przeliczyć jednostki dla reprezentatywnych fragmentów lotu i sprawdzić graficznie wartości doskonałości w poszczególnych stanach lotu. Na wykresie barogramki kąt szybowania wyraźnie się zwiększa przy wciśnięciu speeda i można tą wartość przenieść na nowy wykres. Wyraźnie widać na nim, jak zmniejsza się doskonałość z początkowego 9,6 przy prędkości trymowej do 7,6 przy V ½ max i 5,9 dla V max. Dane uśrednione posłużyły też do odręcznego wykreślenia krzywej biegunowej. Po jej wykreśleniu można było określić wartość V min na nieco powyżej 1 m/s ( około 1, 05 m/s ). Można ją uzyskać w przedziale prędkości pomiędzy 33 a 38 km/h. Przy większym zahamowywaniu skrzydła wyniki były trudne do interpretacji, ponieważ skrzydło wykazywało się lotem „ pompującym „ przez co wyniki były trudne do uśrednienia. W tych warunkach V min została określona na 25 km/h przy 1,7 m/s opadania. Linia prosta wychodząca z początku układu współrzędnych i styczna do krzywej biegunowej wskazuje V opt na 41 km/h. Jak widać na wykresie linia ta jest na sporym odcinku biegunowej prawie równoległa do niej i ten odcinek możemy z pewnym przybliżeniem przyjąć jako optymalną doskonałość glajta. Ja przyjąłem tutaj odcinek pomiędzy 38 a 46 km/h. Znaczenie praktyczne dla nas ma to takie, że lecąc z wciśniętym speedem w 1/3 dolecimy w to samo miejsce, co przy leciutko przyhamowanym glajcie. Czyli lecimy szybciej , ale nie kosztem zwiększonej utraty wysokości. Dopiero przy połówce speeda widać wyraźniejszą utratę doskonałości. Skoro jest tak dobrze, to dlaczego nie trymuje się skrzydeł na 45 km/h. Okazuje się, że skrzydła cierpią na pewną dolegliwość. Jeśli lecimy na speedzie i dostaniemy klapę, to skrzydło wchodzi w rotację. Jeśli nie puścimy speeda, czyli nie przyhamujemy skrzydła zmianą kąta natarcia, to dolegliwość zmienia się w śmiertelną chorobę. Dlatego nie spotkałem do tej pory skrzydeł trymowanych na prędkość powyżej 40 km/h bez speeda. Widocznie nawet zawodnikom trzeba dać szansę przeżycia.
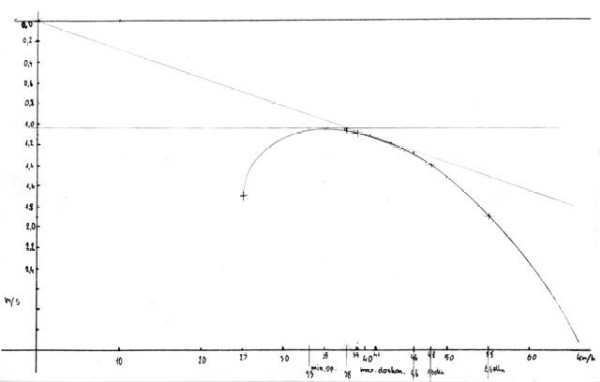
Mając taki wykres krzywej biegunowej możemy wyregulować sobie speeda. Dobrze jest mieć rozwiązanie pozwalające uzyskać dwie prędkości na przyspieszaczu. Pierwszą będziemy używać dla uzyskania maksymalnego zasięgu w słabych duszeniach i przy słabych wiatrach przeciwnych, a drugi bieg wrzucamy poganiani przez silniejsze przeciwności.
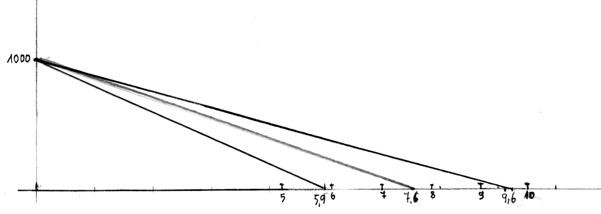
Dzięki wykresowi krzywej biegunowej możemy poznać wartości liczbowe przeciwności, przy jakich wykorzystamy poszczególne belki przyspieszacza.
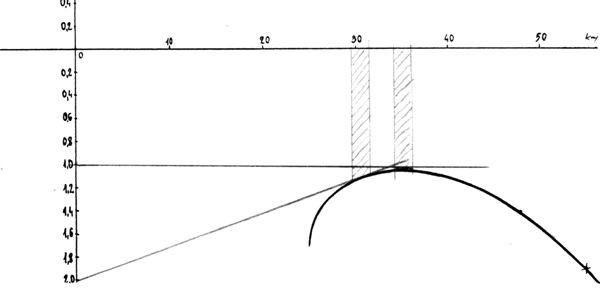
Wyliczenie optymalnej prędkości w duszeniach dokonujemy na wykresie przeprowadzając styczną do interesującego nas punktu na krzywej. Ten punkt informuje nas o prędkości najlepszej doskonałości, a drugi koniec prostej wskazuje wartość duszenia dla którego wskazana prędkość jest prędkością optymalną. Widać na wykresie lotu w duszeniach dwie proste styczne w punktach biegunowej otrzymanych na pierwszej i drugiej belce speeda. Odczytujemy z wykresu, że przy locie na pierwszej belce mamy najlepszą doskonałość w duszeniu 1,2 m/s. Wariometr będzie wtedy wskazywał opadanie 2,2 m/s. Oznacza to przy takim właśnie duszeniu najlepiej wcisnąć pół speeda. Analogicznie drugą belkę najlepiej będzie wcisnąć, gdy opadanie na wariometrze przekroczy 3,6 m/s.
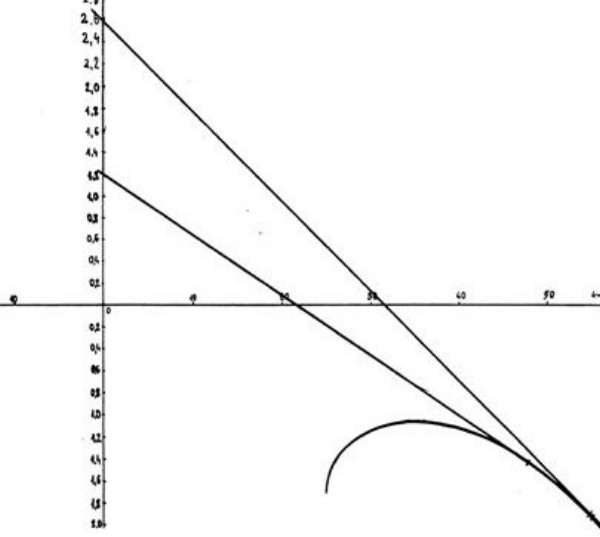
Podobny proces przeprowadzamy dla przeciwnego wiatru. Styczne do krzywej wskażą nam, że na pierwszej belce osiągniemy maksymalną doskonałość przy wietrze czołowym 21 km/h, a na drugiej 30 km/h.
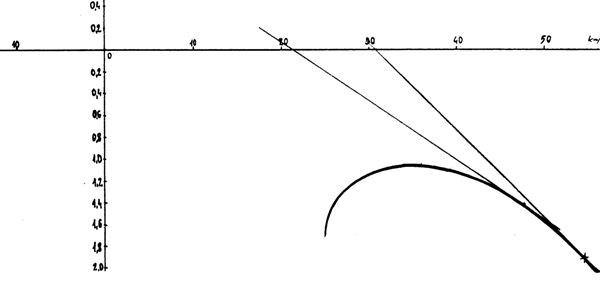
Poza wskazanymi prędkościami doskonałość będzie mniejsza. Dlatego, jeśli na dolocie pod wiatr wiejący z prędkością 20 km/h wciśniemy drugą belkę speeda, to przelecimy mniej, niż na pierwszej belce.
Wykorzystując wykres możemy odpowiedzieć sobie na pytanie jaka będzie optymalna prędkość dla wiatru przeciwnego wiejącego z prędkością 10 km/h. Prosta styczna do krzywej biegunowej będzie się wtedy zaczynać na wartości 10 km/h po prawej stronie wykresu , a punkt styku na krzywej będzie wskazywał V opt dla tych warunków – w tym przypadku 45 km/h.
Na wykresie przeciwności można sumować i przy wskazaniu na wariometrze opadania 2 m/s przy wietrze czołowym 10 km/h optymalną prędkością będzie 48 km/h, a jeśli wiatr czołowy przy takim samym duszeniu wzrośnie do 20 km/h, to wtedy należy przyspieszyć do 55 km/h.
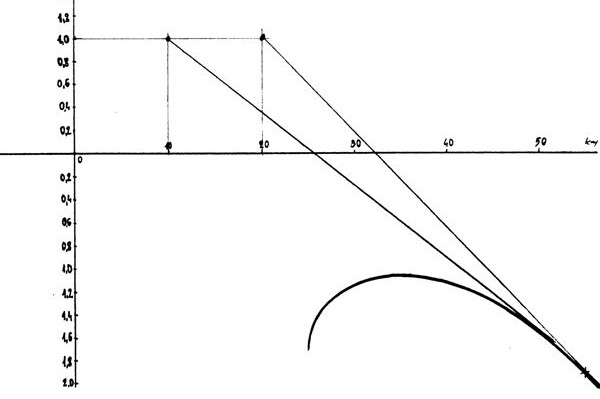
Ciekawą sytuacją jest lot z wiatrem przy duszeniu 2 m/s . Widać wyraźnie, że lepiej wtedy lecieć na pierwszej belce speeda, niż na trymowej.

Prędkość wiatru łatwo odczytać ze wskazań GPS. Podnosząc ręce do góry odczytujemy prędkość względem ziemi, a znając naszą prędkość trymową łatwo możemy wykonać konieczne rachunki w pamięci. Jeśli wskazania prędkości będą wyższe, niż nasza trymowa, to znaczy, że lecimy z wiatrem. Prędkości wiatru po prawej stronie wykresu wskazują nam optymalną prędkość dla takiego lotu. Okazuje się, że nie ma dużej różnicy pomiędzy lotem z wiatrem wiejącym z prędkością 10 km/h, a takim, który wieje 20 km/h. W obu przypadkach najlepiej będzie lecieć na minimalnie przyhamowanym glajcie.
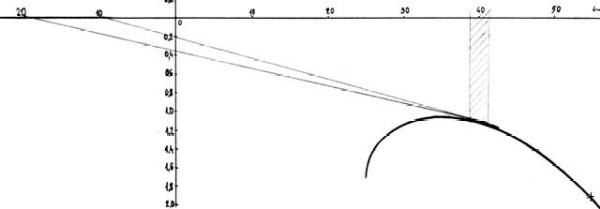
Jeśli przelatujemy przez noszenie, to widać na wykresie, że też powinniśmy przyhamować glajta, aby osiągnąć jak największą doskonałość. W powietrzu wznoszącym się z prędkością 1 m/s wario będzie wskazywało 0 m/s opadania i z wykresu wynika, że ten obszar powinniśmy pokonywać na prędkości ekonomicznej, czyli przy minimalnym opadaniu. Jeśli wario zacznie wskazywać wznoszenie 1 m/s, to należałoby zwolnić do 30 km/h.
Jednak w praktyce są to rzadkie sytuacje, gdyż w noszeniach krążymy i w tej sytuacji potrzebna nam jest prędkość ekonomiczna. Trzeba pamiętać o tym, że wszystkie te prędkości zwiększają się wraz ze wzrostem wysokości. Jeżeli na poziomie morza prędkość najmniejszego opadania wynosiła 35 km/ h, to na wysokości 2000 m wzrośnie do 38,6 km/h. Prędkość maksymalna przekroczy wtedy 60 km/h i to jest cała tajemnica wspaniałych parametrów jakie często odkrywamy w drukach reklamowych.
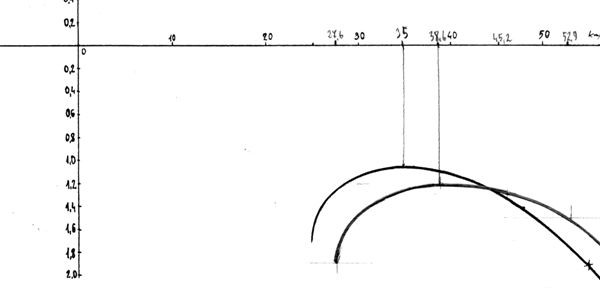
Lecąc swoim glajtem na wysokości 3500 metrów moja prędkość trymowa wahała się pomiędzy 43 a 45 km/h. Jest to praktyczna wskazówka, że jeśli chcemy lecieć szybko, to dobrze jest robić to na jak największej wysokości.
Podobnie jest z obciążeniem powierzchni. Pomiary były robione przez pilota o wadze startowej 109 kg. Ja ważę do startu o 9 kg mniej i musiałem przeliczyć biegunową do swojej wagi. Ponieważ stosunek zarówno prędkości opadania, jak i prędkości lotu po zmianie obciążenia jest równy stosunkowi pierwiastków z wartości obciążenia powierzchni, to łatwo można wyliczyć proporcję, gdzie wartość nowej prędkości liczymy dzieląc iloczyn poprzedniej prędkości i pierwiastek z nowego obciążenia powierzchni prędkości poprzez pierwiastek poprzedniego obciążenia powierzchni. Analogicznie postępujemy przy obliczaniu prędkości opadania. Po wyliczeniu nowych wartości okazało się, że wszystkie wartości ulegną zmniejszeniu gdy ja wsiądę na tego samego glajta. I tak V min spadnie do 24 km/h, opadanie minimalne spadnie do wartości 1m/s przy 33,5 km/h ( poprzednio 35 km/h ), V trymowa zmniejszy się o 1,7 km/h. Prędkość maksymalna spadnie do 52,7 km/h.
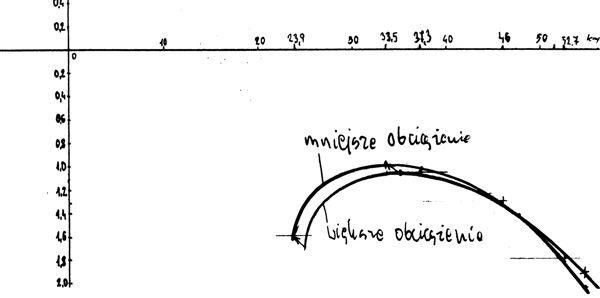
Wszystkie paralotnie latają podobnie, ale nie można automatycznie przenosić zamieszczonych tu danych na swojego glajta. Publikowane dane odnoszą się jedynie do paralotni Shark z firmy Dudek Paragliding. Aby opracować taktykę przelotową na swoim skrzydle każdy pilot powinien starać się wydobyć krzywą biegunową swojego glajta od producenta, lub zrobić ją samemu. W tym drugim przypadku odpadnie nam przeliczanie krzywej dla naszego obciążenia powierzchni. Firmy paralotniowe niechętnie udostępniają wyniki pomiarów w locie, ponieważ piloci nie potrafią wykorzystywać wykresu krzywej biegunowej do latania, natomiast świetnie potrafiliby podważać wartość danego modelu na podstawie wyłącznie oceny osiągów. Mam nadzieję, że dzięki temu artykułowi paralotniarze bardziej świadomie będą dyskutować na temat osiągów swoich skrzydeł.